Треугольники — это трехсторонние замкнутые многоугольники, образованные пересечением трех прямых. Это часто встречается в повседневной жизни. Это одна из основных форм геометрии. У него три стороны, три угла и три вершины. Прямоугольный треугольник — это такой, в котором один из углов всегда равен 90°. Теорема Пифагора выведена для прямоугольных треугольников, которая гласит, что квадрат гипотенузы (самой длинной стороны) равен сумме квадратов основания и перпендикуляра.
Учитывая длину по крайней мере двух сторон прямоугольного треугольника, мы можем найти значение любого угла прямоугольного треугольника. Для этого мы используем различные тригонометрические функции, такие как синус, косинус, тангенс, котангенс, сек и cosec. Они помогают нам соотнести углы прямоугольного треугольника с его сторонами. Кстати, найдите угол при большем основании на страницах специализированного сайта.
Свойства
- Среди трех вершин есть прямоугольная вершина
- Сторона, противоположная прямоугольной вершине, называется гипотенузой.
- Длина сторон соответствует теореме Пифагора, которая гласит
гипотенуза2 = основание 2 + высота 2
- Гипотенуза — это самая длинная сторона прямоугольного треугольника.
- Углы, отличные от прямого угла, являются острыми, поскольку их значение меньше 90o
Тригонометрические функции
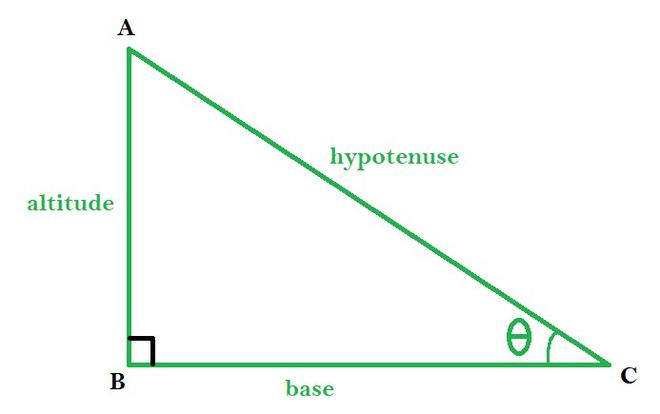
ABC — прямоугольный треугольник с ∠B в качестве прямого угла
- COSθ: Это дает отношение основания к гипотенузе прямоугольного треугольника.
cosθ = основание / гипотенуза
- sinθ: Это дает отношение высоты к гипотенузе прямоугольного треугольника.
sinθ = высота / гипотенуза
- Загарθ: Это отношение высоты к основанию прямоугольного треугольника.
Загарθ = высота / основание
- cotθ: это обратная величина к Tanθ
- Секундаθ: Это величина, обратная cosθ
- Косекθ: это величина, обратная sinθ
Чтобы найти углы прямоугольного треугольника, мы можем взять тригонометрическую величину, обратную отношению заданных сторон треугольника.
Пример:
Если sinθ = x, то мы можем записать
θ = sin-1x.
Это возвращает угол, для которого синусоидальное значение угла равно x.
Аналогично, существуют cos -1θ, tan-1θ, cot-1θ, sec-1θ и cosec-1θ
Примеры задач
Вопрос 1. Задан прямоугольный треугольник, основание которого равно 10 см, а гипотенуза равна 20 см. Найдите значение базового угла.
Решение:
Дано основание = 10 см
Гипотенуза = 20 см
Пусть значение базового угла равно θ. Мы можем записать
cosθ = основание / гипотенуза = 10/20 = 1/2
θ = cos-1(1/2) = 60o
Таким образом, значение базового угла равно 60o.
Вопрос 2. Найдите значение углов прямоугольного треугольника, учитывая, что один из острых углов в два раза больше другого.
Решение:
Поскольку мы знаем, что сумма всех трех углов в треугольнике равна 180o.
Поскольку один из углов равен 90o, а один из острых углов в два раза больше другого, мы можем рассматривать их как θ и 2θ.
Итак, мы можем написать
90o + θ + 2θ = 180o
3θ = 180o – 90o
3θ = 90o
θ = 90o/3 = 30o
2θ = 2 × 30o = 60o
Итак, углы равны 30o, 60o и 90
Вопрос 3. Найдите значение угла подъема лестницы длиной 5 м, учитывая, что основание лестницы находится на расстоянии 3 м от стены.
Решение:
Поскольку лестница действует как гипотенуза прямоугольного треугольника, а расстояние до основания равно 3 м, мы можем записать
Гипотенуза = 5 м
Основание = 3 м
Пусть угол возвышения равен θ. Итак, мы можем записать
cosθ = Основание / гипотенуза = 3/5
θ = cos-1(3/5)
θ = 53o
Таким образом, значение угла возвышения равно 53o.
Вопрос 4. Найдите значение гипотенузы, учитывая, что длина высоты равна 8 м, а базовый угол равен 30o.
Решение:
Учитывая, что базовый угол равен 30o, а высота равна 8 м, мы можем применить функцию синуса, чтобы найти длину гипотенузы.
sin30o = высота / гипотенуза
гипотенуза = высота / sin30o
Поскольку значение sin30o равно 1/2, мы можем записать
гипотенуза = высота / (1/2) = 2 × высота
Таким образом, гипотенуза = 2 × 8 = 16m
Таким образом, длина гипотенузы равна 16 м.